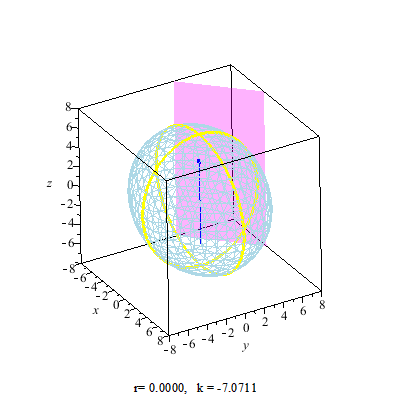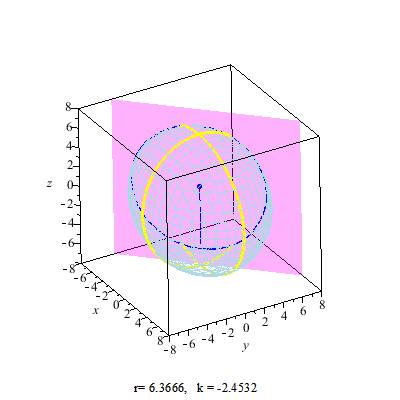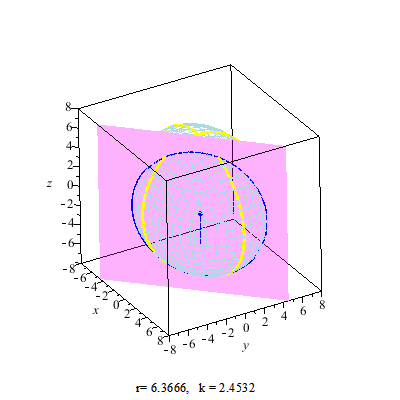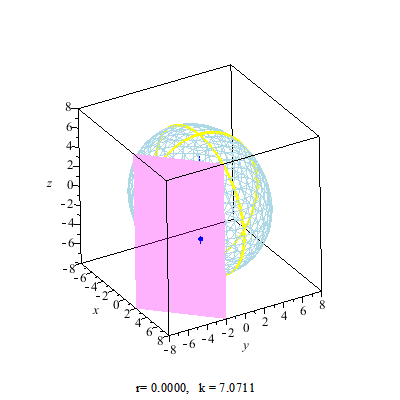
Ellipsoid Circular Section
An ellipsoid is a closed quadric surface that is a three-dimensional analogue of an ellipse. The standard equation of an ellipsoid centered at the origin of a Cartesian coordinate system and aligned with the axes is
Generalised equations
More generally, an arbitrarily oriented ellipsoid, centered at v, is defined by the solutions x to the equation
where A is a positive definite matrix and x, v are vectors.
The eigenvectors of A define the principal axes of the ellipsoid and the eigenvalues of A are the reciprocals of the squares of the semi-axes: 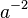 ,
,  and
and  .[1] An invertible linear transformation applied to a sphere produces an ellipsoid, which can be brought into the above standard form by a suitable rotation, a consequence of the polar decomposition (also, see spectral theorem). If the linear transformation is represented by a symmetric 3-by-3 matrix, then the eigenvectors of the matrix are orthogonal (due to the spectral theorem) and represent the directions of the axes of the ellipsoid: the lengths of the semiaxes are given by the eigenvalues. The singular value decomposition andpolar decomposition are matrix decompositions closely related to these geometric observations.
.[1] An invertible linear transformation applied to a sphere produces an ellipsoid, which can be brought into the above standard form by a suitable rotation, a consequence of the polar decomposition (also, see spectral theorem). If the linear transformation is represented by a symmetric 3-by-3 matrix, then the eigenvectors of the matrix are orthogonal (due to the spectral theorem) and represent the directions of the axes of the ellipsoid: the lengths of the semiaxes are given by the eigenvalues. The singular value decomposition andpolar decomposition are matrix decompositions closely related to these geometric observations.
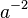 ,
,  and
and  .[1] An invertible linear transformation applied to a sphere produces an ellipsoid, which can be brought into the above standard form by a suitable rotation, a consequence of the polar decomposition (also, see spectral theorem). If the linear transformation is represented by a symmetric 3-by-3 matrix, then the eigenvectors of the matrix are orthogonal (due to the spectral theorem) and represent the directions of the axes of the ellipsoid: the lengths of the semiaxes are given by the eigenvalues. The singular value decomposition andpolar decomposition are matrix decompositions closely related to these geometric observations.
.[1] An invertible linear transformation applied to a sphere produces an ellipsoid, which can be brought into the above standard form by a suitable rotation, a consequence of the polar decomposition (also, see spectral theorem). If the linear transformation is represented by a symmetric 3-by-3 matrix, then the eigenvectors of the matrix are orthogonal (due to the spectral theorem) and represent the directions of the axes of the ellipsoid: the lengths of the semiaxes are given by the eigenvalues. The singular value decomposition andpolar decomposition are matrix decompositions closely related to these geometric observations.Parameterization
The surface of the ellipsoid may be parameterized in several ways. One possible choice which singles out the 'z'-axis is:
where
The parameters may be interpreted as spherical coordinates. For constant u, that is on the ellipse which is the intercept with a constant z plane, v then plays the role of the eccentric anomaly for that ellipse. For constant v on a plane through the Oz axis the parameter u plays the same role for the ellipse of intersection. Two other similar parameterizations are possible, each with their own interpretations. Only on an ellipse of revolution can a unique definition of reduced latitude be made.
Tri-axial ellipsoid with distinct semi-axes a, b and c
Volume and surface area
Volume
The volume of the internal part of the ellipsoid is
Note that this equation reduces to that of the volume of a sphere when all three elliptic radii are equal, and to that of an oblate or prolate spheroid when two of them are equal.
The volume of an ellipsoid is two thirds the volume of a circumscribed elliptic cylinder.
The volume of an ellipse of dimension higher than 3 can be calculated using the dimensional constant given for the volume of a hypersphere. One can also define ellipsoids in higher dimensions, as the images of spheres under invertible linear transformations. The spectral theorem can again be used to obtain a standard equation akin to the one given above.
Surface area
The surface area of a general (tri-axial) ellipsoid is
-

- where

and where F(φ,k) and E(φ,k) are incomplete elliptic integrals of the first and second kind respectively.
The surface area of an ellipsoid of revolution (or spheroid) may be expressed in terms of elementary functions:
which, as follows from basic trigonometric identities, are equivalent expressions (i.e. the formula for  can be used to calculate the surface area of a prolate ellipsoid and vice versa). In both cases e may again be identified as the eccentricity of the ellipse formed by the cross section through the symmetry axis. (See ellipse). Derivations of these results may be found in standard sources, for example Mathworld.
can be used to calculate the surface area of a prolate ellipsoid and vice versa). In both cases e may again be identified as the eccentricity of the ellipse formed by the cross section through the symmetry axis. (See ellipse). Derivations of these results may be found in standard sources, for example Mathworld.
 can be used to calculate the surface area of a prolate ellipsoid and vice versa). In both cases e may again be identified as the eccentricity of the ellipse formed by the cross section through the symmetry axis. (See ellipse). Derivations of these results may be found in standard sources, for example Mathworld.
can be used to calculate the surface area of a prolate ellipsoid and vice versa). In both cases e may again be identified as the eccentricity of the ellipse formed by the cross section through the symmetry axis. (See ellipse). Derivations of these results may be found in standard sources, for example Mathworld.
To be Continue

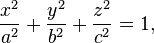





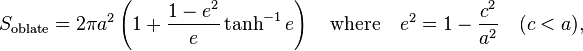



0 komentar:
Posting Komentar